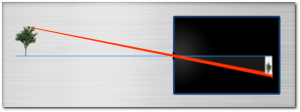
Some centuries ago, people noticed with some surprise, that in a dark room sometimes an (upside down) image of the environment is projected across a small opening in a wall.
The old latin word for room (chamber) is camera.
That’s why the first cameras got the name “camera obscura” ( = “dark chamber”). One of the first real-life-applications was portrait painting.
The same principle is used in so called “pinhole-cameras”: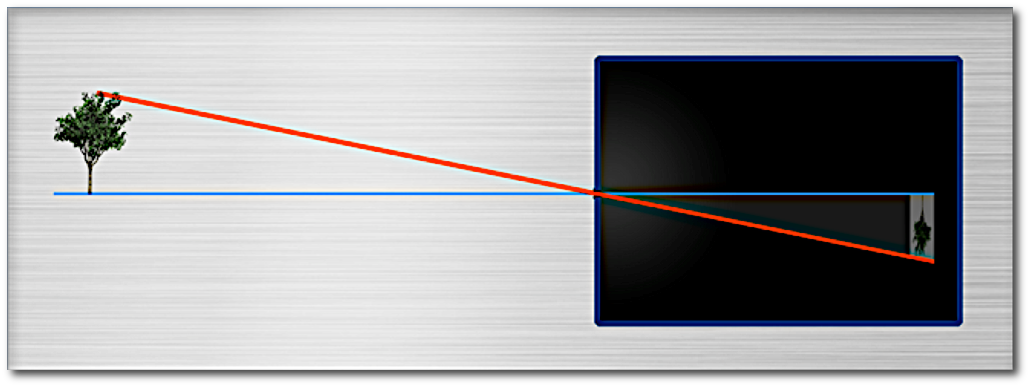
Its immediately clear, why the image is upside down.
The advantage is however, that the Image is were it would be mathematically expected. There is no distortion ! (rectangles on object side becomae rectangles on image side). There’s no visible dependency from the wavelength. The depth of Field is infinitely large.
The disadvantage is that the resulting image is very dark, (so the room must be even darker for the image to be seen at all. The needed exposure times to take an image with todays cameras could well be minutes!
Idea: Lets use a larger hole :
Now, however, the image not only gets brighter (as intended) but also gets blurry, because the light not only passes through the center of the hole. So not only the correct position of the image is exposed to the light, but also the direct neighbours.
As a result, the image of an object point is not just a point, but instead a little disk, the so called “Circle of Confusion” (CoC).
For short distance objects, even larger. Read, the “resolution” is very bad.
Whish: Each image point shall be just a mathematical point and not a circle.
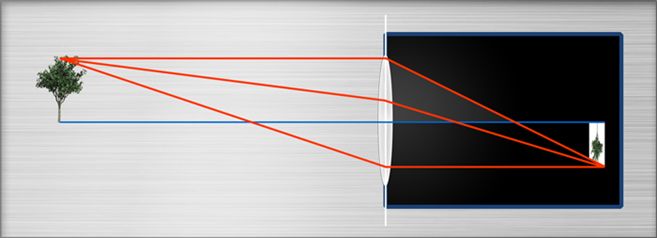
Idea: lets place a biconvex (“collecting lens”) lens into the hole:
How to predict what size the image will have and where the position of the Images of object points is?
Two simple rules apply:
Rays through the center of the lens pass straight through the lens.
Rays arriving parallel to the optical axis and through the object point are “bent” through the focal point of the lens.
Where these two rays meet, is the image of the object point.
We note:
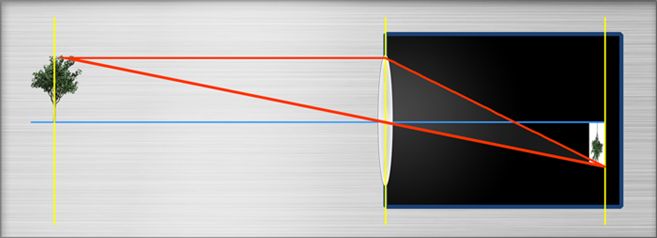
If image and object distnces are given, we can calculate the focal length of the lens.
This appoach is used in all them focal length calculators online.
In real life, we notice a slight difference between the theoretical values and the real distances: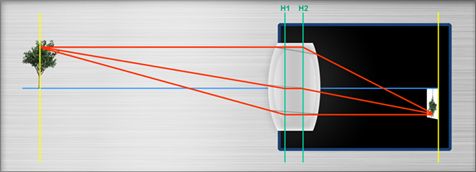
Due to this difference between theory and parctice :
But even the model of the thick lenses (the “paraxial image model”) works with
The lenses are perfect, say don’t have optical aberrations.
In case of the thin lenses : all lenses are infinitely thin.
Monochrome light is used.
The model assumes sin(x) = x, which is an approximation that holds only very close to the optical axis.
There’s good and bad news :
We also notice that :
Objects at different distances result in CoCs of different size.
The “acceptable” maximal size of the CoC thus results in the so called “depth of field”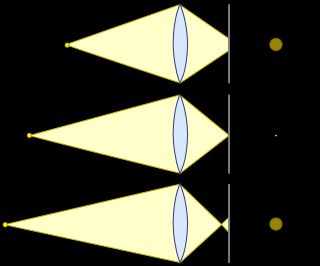
Say : there are no perfect lenses. (even if they could be produced arbitrarily accurate)
The theoretical size of the smallest CoC possible even for close to perfect lenses , so called diffraction limited lenses) is described by the so called Rayleigh criterion.
For white light it’s not possible to generate CoCs smaller than the F# measured in micrometers.
The theoretical resultution is half thatvalue
The theoretical best resultion is 4um / 2 = 2um
See also Why can color cameras use lower resolution lenses than monochrome cameras?.
If the image can appear focussed on a sensor with n megapixels, then the lens is classified as an n Megapixel lens